Fonctions mathématiques en 1ère S : Guide complet

Cours de 1ère S sur la trigonométrie Le plan est muni d’un repère orthonormé Cosinus et sinus Soit t un nombre réel et M le point repéré par le nombre t sur le cercle trigonométrique C. Le cosinus de t, noté cos(t) et le sinus de t, noté sin(t), sont respectivement l’abscisse et l’ordonnée de M dans le repère. Les fonction définies sur ℝ par : . S’appellent les fonctions cosinus et sinus. On les obtient sur la calculatrice réglée…

Exercices corrigés à imprimer pour la 1ère S sur la trigonométrie Cosinus et sinus d’un réel Exercice 01 : Sinus Soit t un nombre réel vérifiant a. A l’aide du cercle trigonométrique, donner le signe de sin(t). Calculer la valeur exacte de sin(t). b. Mettre la calculatrice en mode radian et donner une valeur approchée du nombre t. Exercice 02 : Cosinus Soit t un nombre réel vérifiant a. A l’aide du cercle trigonométrique, donner le signe de cos(t). Calculer…

Cours de 1ère S sur les angles orientés et le cercle trigonométrique Le plan est muni d’un repère orthonormé Cercle trigonométrique Le cercle trigonométrique C de centre O est le cercle de rayon 1, orienté positivement (dans le sens inverse des aiguilles d’une montre). Angle orienté On appelle I, J, et I’ les points définis par : Soit M un point du cercle trigonométrique. Les vecteurs et dans cet ordre définissent un angle orienté de vecteurs noté . L’angle orienté…

Exercices corrigés à imprimer pour la 1ère S Cercle trigonométrique et angles orientés Exercice 01 : Repérage Placer les point A, B, C et du cercle trigonométrique repérés respectivement par les nombres réels : Exercice 02 : Placer des points a. Rappeler comment placer un point image sur un cercle trigonométrique ? b. Construire un cercle trigonométrique et placer les points images des nombres réels suivants :…..   Voir les fichesTélécharger les documents Angles orientés – Cercle trigonométrique – 1ère…

Cours de 1ère S – Mesure d’un angle orienté de deux vecteurs non nuls Le plan est muni d’un repère orthonormé Angle orienté de deux vecteurs non nuls Soit A et B deux points du cercle trigonométrique C. Si a est une mesure de et b une mesure de , alors les mesures en radians de l’angle orienté sont les nombres b – a + k x 2π, où k est un nombre entier relatif. On note: = b –…

Exercices à imprimer avec correction pour la première S Mesure d’un angle orienté de deux vecteurs non nuls – Trigonométrie Exercice 01 : Avec des triangles. Dans le plan orienté, on a construit : Un triangle ABC tel que : Un triangle ACD équilatéral tel que. Le point L est le milieu de [BC] et le point K est le milieu de [DC]. a. Donner la mesure principale en radians de chacun des angles orientés : b. Démontrer que le…

Cours de 1ère S – Mesure d’un angle orienté – radian Le plan est muni d’un repère orthonormé Repérage d’un point Pour repérer un point M sur le cercle trigonométrique, on imagine l’enroulement d’une droite graduée (avec la même unité que celle des axes du repère) autour du cercle à partir du point I. Soit un réel t, abscisse d’un point de la droite s’applique sur M. Ce réel t repère M sur le cercle trigonométrique C. Le radian….. Mesures…

Exercices corrigés à imprimer pour la première S Radian, Mesure d’un angle orienté Exercice 01 : Radians et degrés Soit M un point du cercle trigonométrique. On note t la mesure en radians de l’angle orienté appartenant [0 ; 2π[ et α la mesure en degrés de l’angle au centre . Les nombres t et α sont liés par la formule . a. Donner la mesure en degrés des angles dont une mesure en radians est . b. Donner une…

Cours de 1ère S sur la dérivée f’ de f Dérivée f’ de f Soit f une fonction définie et dérivable sur un intervalle I et f et f’ sa fonction dérivée. Théorème: f est croissante sur I si, et seulement si, f’ est positive sur I. f est décroissante sur I si, et seulement si, f’ est négative sur I. f est constante sur I si, et seulement si, f’ est nulle sur I. Exemple d’application : Solution :…

Exercices à imprimer pour la première S sur la dérivée f’ de f Exercice 01 : Soit la fonction f définie sur R par : C sa courbe représentative dans un repère orthogonal. Calculer la dérivée de. Etudier le signe de selon les valeurs de x et en déduire le sens de variation de. Calculer une équation de la tangente T à la courbe C au point d’abscisse 0. En déduire une valeur approchée de. Tracer la courbe C, ses…

Cours de 1ère S sur les fonctions: les opérations Opération sur les fonctions On considère une fonction u définie sur un intervalle I. Soit k un nombre réel. Les fonctions u et u + k ont le même sens de variation sur l’intervalle I. Soit λ Un nombre réel. Si, alors les fonctions u et ont le même sens de variation sur l’intervalle I. Si, alors les fonctions u et ont des sens de variation contraires sur l’intervalle I….. Exemple…

Exercices à imprimer de première S : Opérations sur les fonctions Exercice 01 : Soit la fonction f définie sur par : Première partie : Etudier les variations de f et tracer sa représentation graphique C dans un repère orthonormé Montrer que C est un demi-cercle de centre A (0 ; 1). Déterminer les abscisses des points d’intersection de C avec la droite. Deuxième partie : On considère la famille de fonction f1, f2 associées à la fonction f définies…

Cours de 1ère S sur la définition d’une fonction croissante ou décroissante sur un intervalle Croissance et décroissance d’une fonction sur un intervalle Soient deux nombres réels a et b dans un intervalle. On suppose que. Pour déterminer le sens de variation d’une fonction f, on compare soit en manipulant les inégalités, soit en étudiant le signe de la différence. Utilisation d’une calculatrice ou d’un logiciel Application à travers un exemple: Soit la fonction f définie sur par Afficher la…

Exercices à imprimer pour la première S Définition d’une fonction croissante ou décroissante sur un intervalle Exercice 01 : Pour résoudre l’équation, on utilise une calculatrice. On a affiché la courbe représentative de la fonction cube et des tableaux des valeurs.Graphiquement, l’équation admet une seule solution c. Déterminer des encadrements de c d’amplitude 0.1 et 0.01. Développer. Soit f la fonction définie sur R par Etudier les variations de f et dresser son tableau de variations. Donner la valeur exacte…

Cours de 1ère S sur le sens de variation On considère une fonction u définie sur un intervalle I. Dans un plan muni d’un repère on note Cu la courbe représentative de u La fonction u+k La fonction notée u+k est la fonction définie sur I par Les fonctions u et u+k ont le même sens de variation sur l’intervalle I. La courbe Cu+k est l’image de la courbe Cu par la translation de vecteur La fonction λu La fonction…

Exercices à imprimer pour la première S sur le sens de variation Exercice 01 : Soit la fonction u définie sur R par : Préciser le sens de variation de u et étudier le signe de u(x) selon les valeurs de x Soit la fonction f définie par : Quel est l’ensemble de définition de f ? Etudier le sens de variation de f Exercice 02 : Soit la fonction u définie sur R par Préciser le sens de variation…

Cours de 1ère S sur le nombre dérivé Taux d’accroissement d’une fonction Soit f une fonction définie sur un intervalle I, a et b deux nombres réels distincts de I. on pose h = b – a, ce qui permet d’écrire b = a + h. Le taux d’accroissement de f entre a et a + h est le nombre : Nombre dérivé d’une fonction en un point Le nombre dérivé de f en a est la limite, si elle…

Exercices à imprimer pour la première S sur le nombre dérivé Exercice 01 : Nombre dérivé Soit f la fonction définie sur ℝ par f(x) = 2×2 + 4x – 6 a. Calculer le taux d’accroissement de f entre 4 et 4 + h, où h est un nombre réel quelconque. b. En déduire le nombre dérivé de f en 4. Exercice 02 : Taux d’accroissement Soit g la fonction définie sur par a. Calculer le taux d’accroissement de g…

Cours de 1ère S sur le calcul des dérivées Fonction dérivée Soit f une fonction définie sur un intervalle I. Si f est dérivable pour tout x de I, on dit que f est dérivable sur I. La fonction dérivée de f est la fonction qui à tout x de I associe le nombre . Dérivées des fonctions usuelles Le tableau suivant regroupe les fonctions usuelles et leurs dérivées. Dérivée d’une somme, d’un produit Soit u et v deux fonctions…

Exercices à imprimer pour la première S sur le calcul des dérivées Exercice 01 : Calculer les dérivées des fonctions suivantes. a. f définie sur ℝ par f(x) = 5×4 – 2×3 + 3×2 – x + 7 b. g définie sur par c. h définie sur par Exercice 02 : Vérification   Vérifier les résultats suivants donnés par un logiciel de calcul formel. Fonction – Dérivée Exercice 03 : Calculer la dérivée de la fonction suivante f définie sur…

Cours de 1ère S sur l’utilisation des dérivées Utiliser les dérivées Lien entre le signe de la dérivée et le sens de variation Soit f une fonction définie et dérivable sur un intervalle I et sa fonction dérivée. f est croissante sur I si, et seulement si, est positive sur I. f est décroissante sur I si, et seulement si, est négative sur I. f est constante sur I si, et seulement si, est nulle sur I. Exemple : Extremum…

Exercices à imprimer pour la première S sur l’utilisation des dérivées Exercice 01 : Etude d’une fonction Soit f une fonction définie par et C sa représentative dans un repère. a. Détermine le domaine de définition de la fonction b. Calculer la dérivée de f. en déduire les variations de f. c. Etudier la position de la courbe C par rapport à la droite d d’équation y = 2. d. Tracer la courbe C, la droite d et la droite…

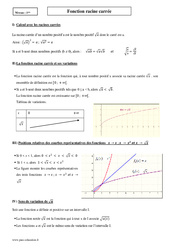
Cours de 1ère S sur la fonction raciné carrée Calcul avec les racines carrées La racine carrée d’un nombre positif a est le nombre positif dont le carré est a. Si a et b sont deux nombres positifs (b ≠ 0), alors : La fonction racine carrée et ses variations La fonction racine carrée est la fonction qui, à tout nombre positif x associe sa racine carrée . son ensemble de définition est . Si a et b sont deux…

Exercices à imprimer pour la première S – Fonction racine carrée Exercice 01 : Simplifier les écritures suivantes Exercice 02 : Opérations avec les racines carrées Exercice 03 : Fonction racine On considère la fonction f définie par a. Calculer les images par f des nombres : – b. Donner l’ensemble de définition de f. c. Etudier le sens de variation de f. Exercice 04: Fonction racine carrée Soit la fonction g définie par a. Déterminer l’ensemble de définition de…

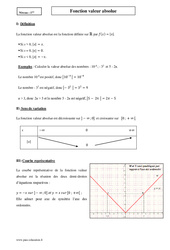
Cours de 1ère S sur la fonction valeur absolue Définition La fonction valeur absolue est la fonction définie sur ℝ par Exemples : Calculer la valeur absolue des nombres : Sens de variation La fonction valeur absolue est décroissante sur et croissante sur Courbe représentative La courbe représentative de la fonction valeur absolue est la réunion des deux demi-droites d’équations respectives :…..   Voir les fichesTélécharger les documents Fonction valeur absolue – Première S – Cours rtf Fonction valeur absolue…

Exercices à imprimer pour la première S sur la fonction valeur absolue Exercice 01 : Calculs avec la valeur absolue a. Calculer la valeur absolue des nombres suivants : b. Ecrire sans le symbole de la valeur absolue où x est un nombre réel quelconque. Exercice 02 : Fonction valeur absolue Soit f une fonction définie par . Etudier et représenter graphiquement la fonction f. Exercice 03 : Démonstration a. Justifier que, pour tout réel x, b. Simplifier les écritures…

Cours de 1ère S sur les fonctions homographiques Etude des fonctions homographiques Fonction inverse: La fonction inverse est la fonction f définie sur R* par : Sens et tableau de variation: Courbe représentative: La courbe représentative de la fonction inverse est une hyperbole. Les fonctions homographiques: Une fonction homographique est une fonction f qui peut s’écrire sous la forme : Exemples :…..   Voir les fichesTélécharger les documents Fonctions homographiques – Première S – Cours rtf Fonctions homographiques – Première…

Exercices à imprimer pour la Première S sur les fonctions homographiques Exercice 01 : Soit la fonction g définie sur R* par : En utilisant le sens de variation de g, compléter les inégalités suivantes : Exercice 02 : Soit la fonction f définie sur : Donner la forme réduite de f. Soit a et b deux réels de, sachant que En déduire le sens de variation de f sur le domaine de définition, tracer le tableau de variation de…

Cours de 1ère S sur les fonctions polynômes de degré 2   Définition et propriétés Soient a, b et c trois nombres réels, avec a ≠ 0. On considère une fonction f définie sur ℝ. On appelle une fonction polynôme de degré deux toute fonction f qui peut s’écrire sous la forme développée f(x) = ax2 + bx + c ; on dit également que f est un trinôme. Si f(x) = ax2 + bx + c, avec a ≠…

Exercices corrigés de première S sur les fonctions polynômes de degré 2 Exercice 01 : Forme canonique Soit le polygone de degré deux x2 – 12x – 5 a. Rappeler le produit remarquable (a – b)2, puis compléter les égalités suivantes : b. Quelle est la forme canonique du polygone Exercice 02 : Etude d’une fonction On considère la fonction f définie sur ℝ par f (x) = 4×2 – 16x. a. Déterminer la forme canonique de f. b. Etudier…